- Stochastic electronematics solver in three dimensional anisotropic fluids under nonuniform electric field.
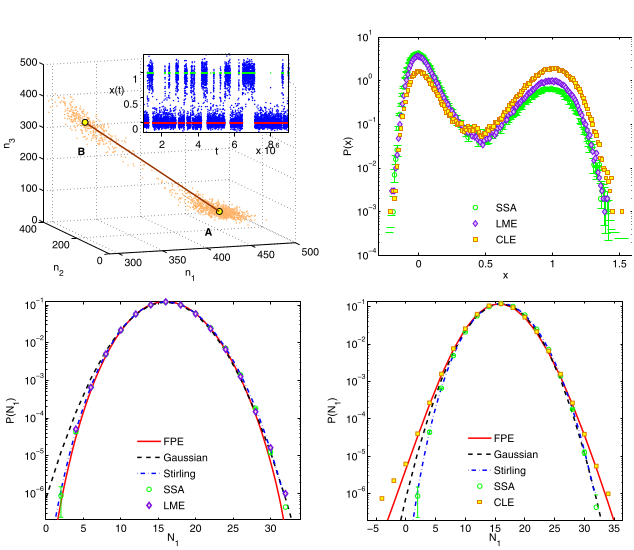
- Kinetic Monte Carlo (SSA) integrator, GENERIC and Chemical Langevin equation (CLE) integrator for dimerization and bistable reactive system.
- Compressible fluctuating hydrodyamics solver for binary reactive gas in 2D/3D using BoxLib.
- Low-Mach number fluctuating hydrodyamics integrator for quasi-incompressible flow in multispecies mixture in 2D/3D using BoxLib.
- Dissipative particle dynamics (DPD) 3D solver for Yukawa and WCA potential with Lees-Edwards (LE) boundary for sheared suspensions.
- Data parallel (cross-platform) uniaxial/biaxial nematic SMOL integrator in three dimensions using GSL, Python and PETSc (implicit and explicit).
- Extensive data-parallel (cross-platform) Allen-Cahn MOL solver in three dimensions (implicit and explicit).
- Stochastic Method of Lines (SMOL) integrator for thermal nematogenic systems.
- (Deterministic) Method of Lines (MOL) (scalar and tensor) integrator using Spectral Collocation Method (SCM).
- Alternate direction implicit (ADI) operator splitting PDE integrator for (active) motor-microtrubule mixture.
Nematic disclinations under non-uniform electric forces and thermal inhibitors
Manipulating topological disclination networks that arise in a symmetry-breaking phase transformation of anisotropic materials
can potentially lead to the design of nove materials like conductive microwires, self-assembled resonators, and active
anisotropic matter. However, progress in this direction is hindered by a lack of control of the kinetics and microstructure
due to inherent complexity arising from competing energy and topology [Figure 1]. Here we have studied thermal and
electrokinetic effects on disclinations in a three-dimensional nonabsorbing nematic material with both signs of the dielectric
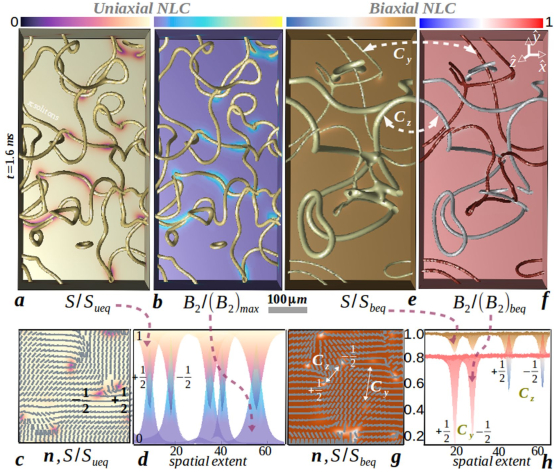
anisotropy. The electric flux lines are found to be highly nonuniform in uniaxial media [Figure 2] after an electric field
below the Fréedericksz threshold is switched on, and the kinetics of the disclination lines is slowed down as seen experimentally.
In biaxial media, depending on the sign of the dielectric anisotropy, apart from the slowing down of the disclination kinetics,
a nonuniform electric field filters out disclinations of different topology by inducing a kinetic asymmetry [Figure 3]. These
results enhance the current understanding of forced disclination networks and establish the presented method (fluctuating
electronematics) as a potentially useful tool for designing materials with novel properties in silico.
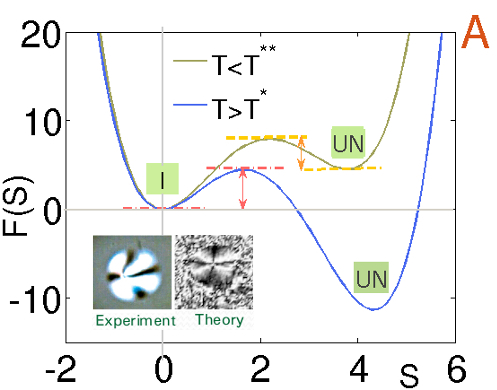
In this work, we utilize our constructed Langevin equations describing the fluctuations of the orientational tensor
that preserves the symmetry and tracelessness of the tensor order, and satisfy Einstein's fluctuation-dissipation
relation at thermal equilibrium, to study nucleation kinetics in quasi two-dimensional nematic film above supercooling
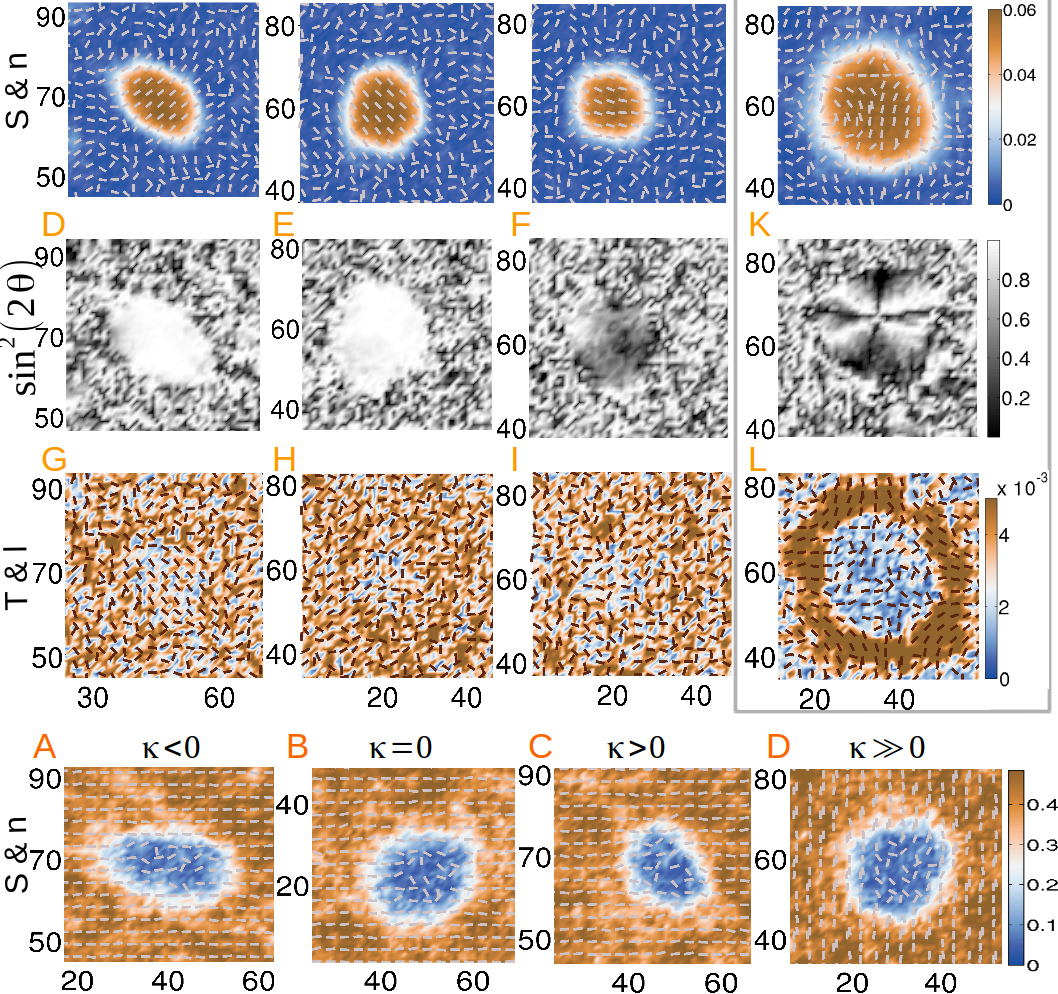
and below superheating limit [Figure 1]. Droplets of nematic (isotropic) order are spontaneous generated in the thermally
fluctuating isotropic (nematic) bath [Figure 4: 3D nematic droplet (vide PhD-Thesis)]. Hyperbolic-hedgehog defect
encapsulated elliptic microdroplets with outer Biaxial rings are formed [Figure 2]. A polynomial dependence on time of
the growth kinetics with drastic violation of the Classical Nucleation Theory (CNT) - as realized through breakdwon of
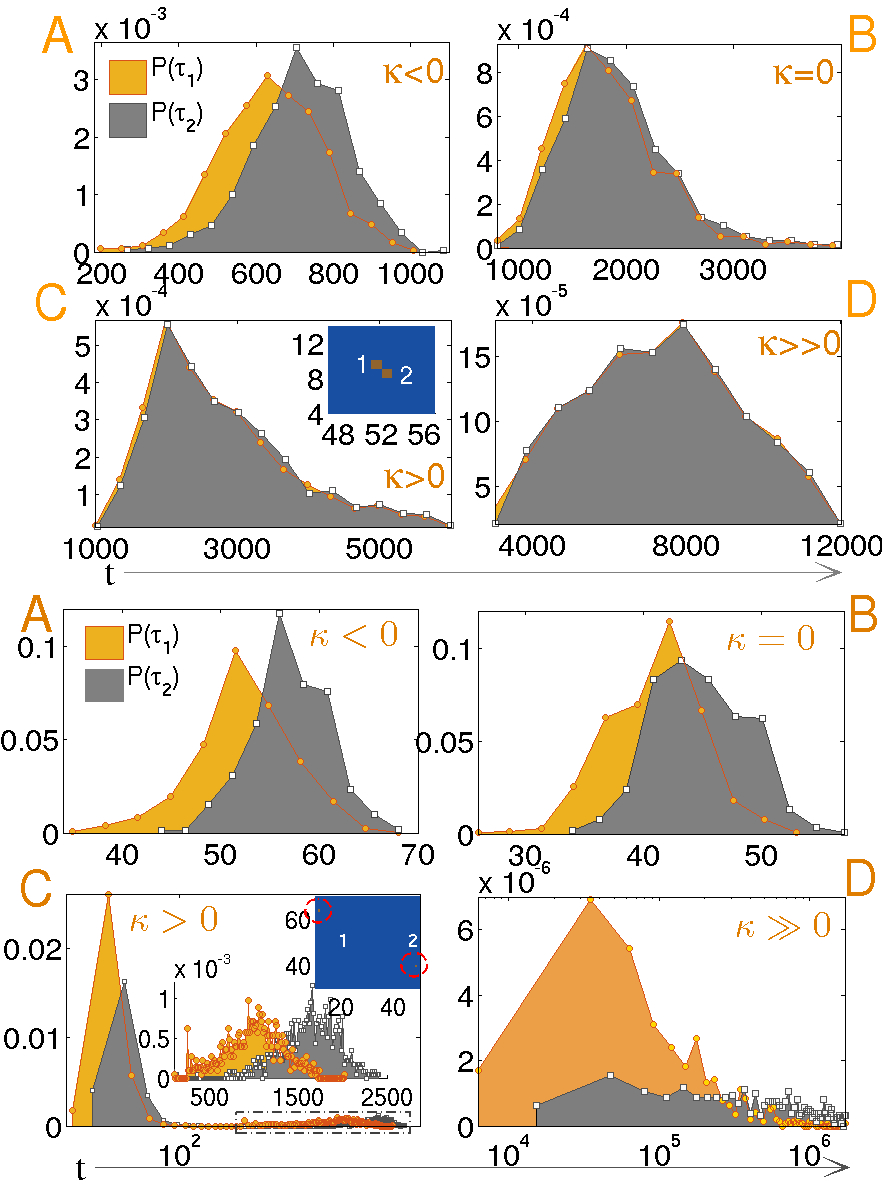
Johnson-Mehl-Avirami-Kolmogorov equation, as well the nucleation rate kinetics - is observed. Spatially distant events
are temporally correlated due to long-ranged elastic interactions [Figure 3]. Two-stage growth process is observed in
isotropic droplets in super-heated nematic film. Details of the numerical formulation, benchmarks and results can be
read in the two articles below & The animations can be viewed
here ,
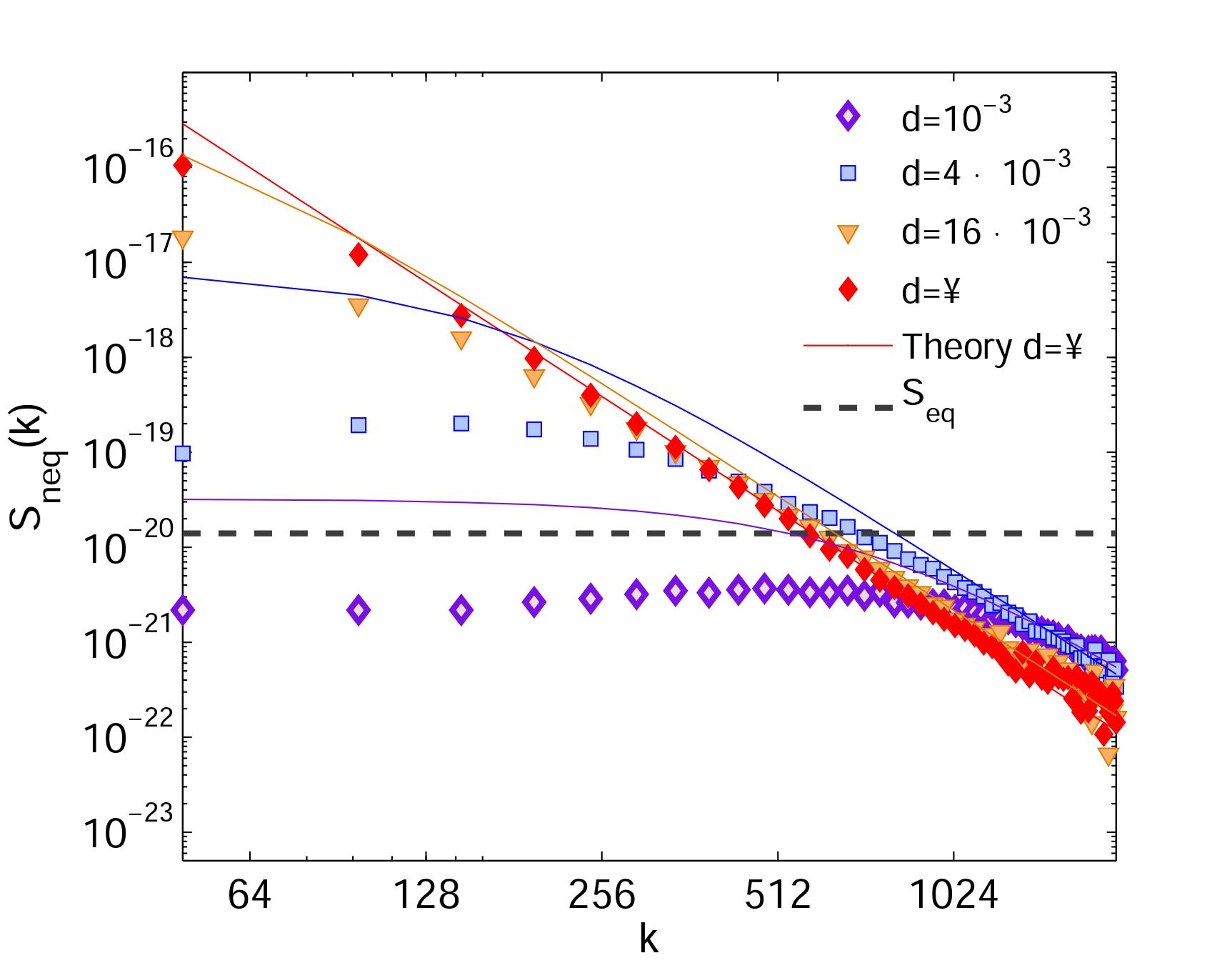
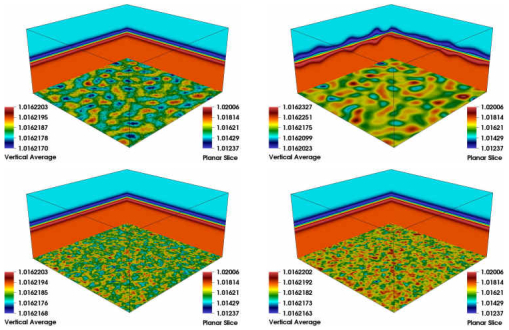
We have formulated a low-Mach number fluctuating hydrodynamics equation for multispecies nonideal liquid,
where fast isentropic fluctuations in pressure are eliminated by replacing the equation of state with a local thermodynamic
constraint. We demonstate of large scale non-equilibrium fluctuation [Figure 1] in the presence of concentration gradients,
reported in light-scattering experiments and shadowgraphy techniques. We had studied mixed-mode instability occuring on the
miscible interface between sugarwater and saltwater in the presence of gravity. The buoyancy driven instability like
double-diffusive effects and Rayleigh-Taylor instability with the mixed-mode instability triggers a fingering
instability of the interface in a Hele-Shaw cell geometry as shown in [Figure 2]. Figure 3 shows the development of
Diffusive Layer Convection (DLC) instability in our computation, when a layer of less-dense salty water is placed on top of
a horizontal layer of denser sweet water. Our findings with detailed numerical methodology is referenced here:
We have studied the nonlinear rheology of a glass-forming binary mixture under the reversal of shear flow using
dissipative particle dynamics simulations that validates Einstein's fluctuation dissipation relation in quiescent
state. Planar Couette flow is established via Lees-Edwards boundary between particles interacting through a
Weeks-Chandler-Andersen potential. Memory effects lead to a history-dependent response of the melt, as
exemplified by the vanishing of a stress overshoot phenomenon in the stress–strain curves of the sheared
liquid, and a change in the apparent elastic coefficients around states with zero stress. The connection of this
macroscopic response to single particle motion is demonstrated via particle mean squared displacement as well
as the self-intermediate scattering function. The results are compared to the schematic mode coupling theory
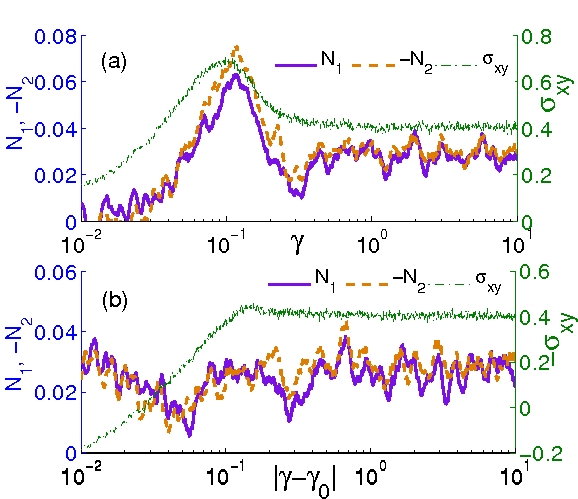
model of sheared glassy liquid where we find excellent agreement with the simulation. Figure(6) shows the
overshoot of shear and normal stress in forward shear and no overshoot at instantaneous shear reversal.
Figure(7) depicts of the local stress on individual particle at a stage where elasto-plastic rearrangements
occur in forward shear while in figure(8), induced anisotropy due to shear is shown in shear-gradient plane,
where particles are squeezed along the compressional axis and extended along the extensional axis. Figure (9)
shows the coarse grained elastic map in forward shear at 1-percent strain, having different regions with higher
and lower elastic constant. The references are inscribed below:
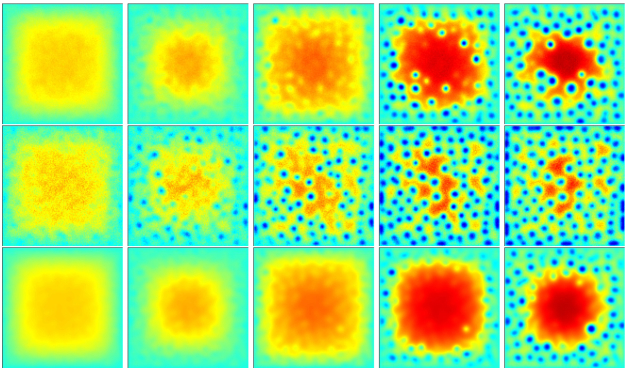
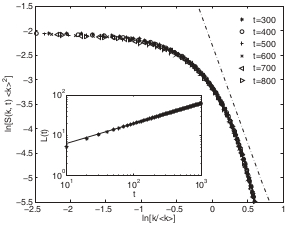
In this work using MOL method, we have performed spinodal kinetics of coarsening following a quench from isotropic
to deep into the nematic phase. We study the scaling behaviour and defect morphology and validate the dynamical scaling with a
clear separation of time scales from diffusive to Porod's law at late stage of the kinetics [Figure 5]. Details of the numerical study,
benchmarks and results are highlighted here:
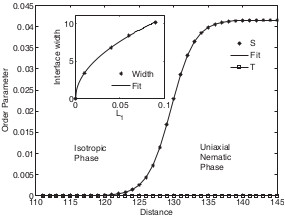
The work describes of statics and kinetics of liquid crystal phase change from liquid to uniaxial/biaxial nematic phase
within the framework of Ginzburg-Landau-deGennes (GLdG) approach. A new deterministic
method of lines (MOL) solution to the dynamic equations of the Q-tensor is presented. We benchmark through the study of
the classic tanh isotropic-nematic interface
at zero temperature [Figure 1]. We perform a stringent test of the
de Gennes ansatz , proposed back in '70s era, and find the condition when the interface remains strictly
uniaxial or partially Biaxial. Benchmarks are reported underneath,



A. K. Bhattacharjee, K. Balakrishnan, A. L. Garcia,
J. B. Bell and A. Donev, J. Chem. Phys. 142, 224107 (2015).

A. Donev, A. J. Nonaka, A. K. Bhattacharjee,
A. L. Garcia and J. B. Bell, Physics of Fluids, 27, 037103 (2015).
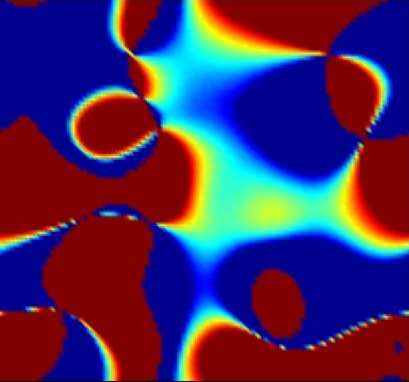
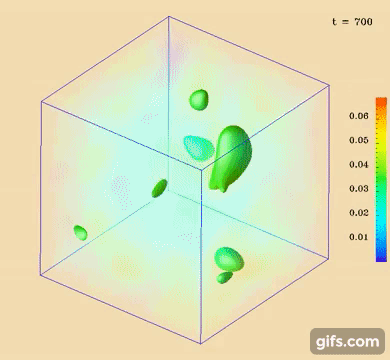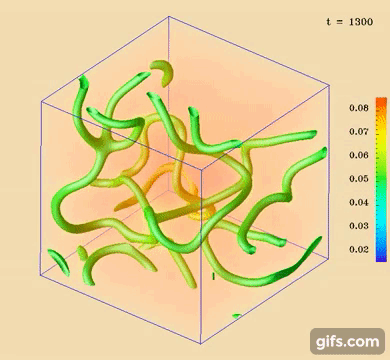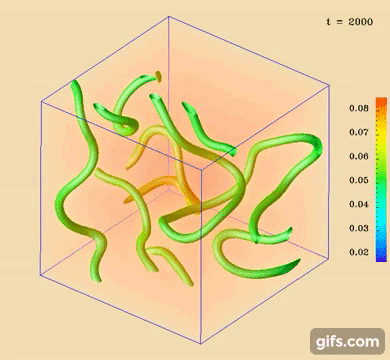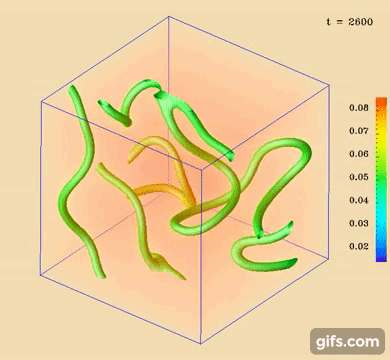
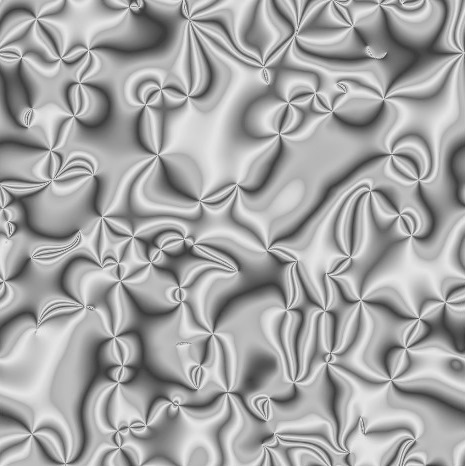
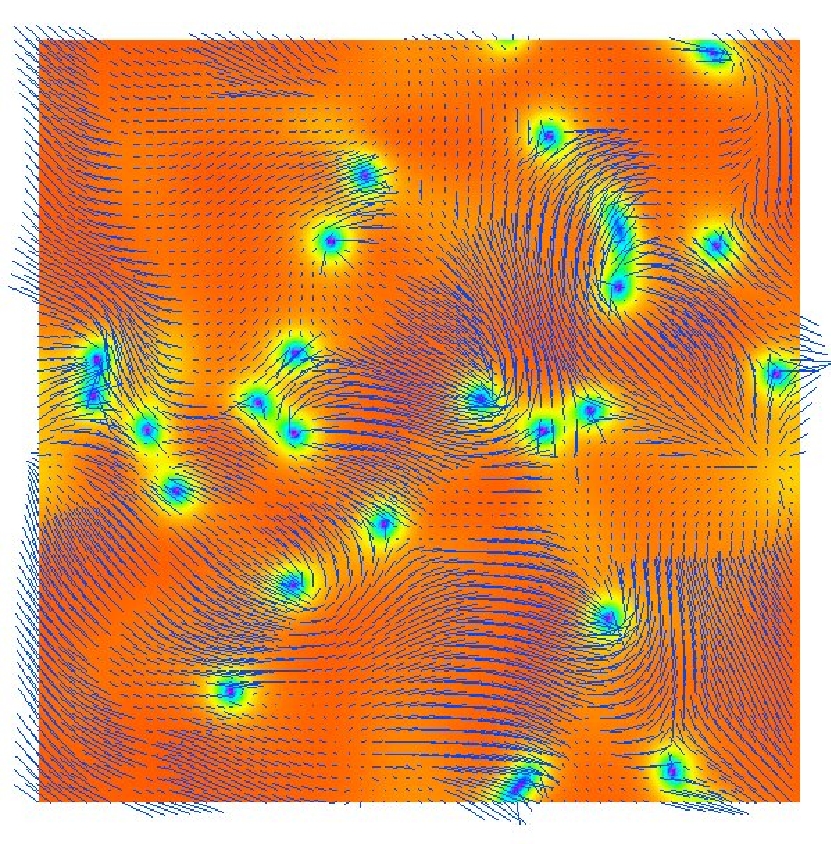

We also have developed new visualization techniques as well as easy defect-finding algorithm, that classifies point and line
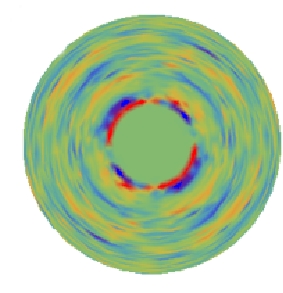
defects in quasi-two and three dimensions [Figure 1], not only via the Schlieren texture [Figure 2] but also by the scalar
order [Figure 3-4]. Both integer, half-integer defects of respective topological class are recognized.
These are animated here ,
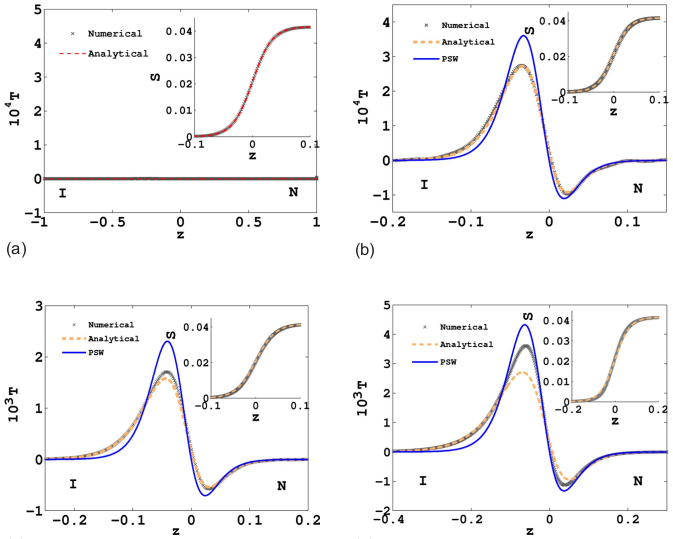

We next develop an extremely accurate collocation scheme for the solution of the
GLdG equations to comment about the nature of the interface as well as the role of anisotropic elastic
constants to the nematic director (planar, homeotropic and oblique) anchoring along the interface [Figure 2]. These
are compared with an approximate analytic exposition and reported in the following articles,
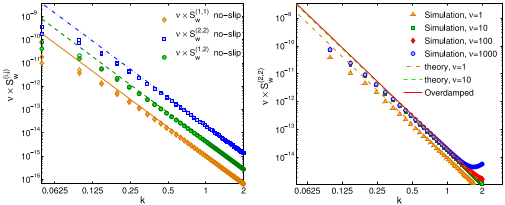
We also perform the stochastic generalization of MOL to examine capillary waves in a thermally fluctuating interface reported
here,